目次
目的
RDKitに実装されているIpc 記述子を理解する。
Ipc(Information content for polynomial coefficients)
RDKitのIpc 記述子は、分子の複雑さを表現した指標であり、以下の論文で定義されています。
D. Bonchev, N. Trinajstic
Chemical Physics 67(10):4517-4533
DOI:10.1063/1.434593
概要
- Ipcは、分子の複雑さ(特に、枝分かれ)を表現した指標です。
- 以下の式で定義されます。
$$
I_{pc} = Z \sum_{i=0}^{n} \frac{|C_i|}{Z} log_2 \frac{|C_i|}{Z} \\
Z= \sum_{i=0}^n |C_i|
$$
ここで、\( C_i \)は化合物の隣接行列の固有多項式における係数を表します。 - また、avgIpc(平均Ipc)は以下の式で定義されます。
$$
avgI_{pc} = \sum_{i=0}^{n} \frac{|C_i|}{Z} log_2 \frac{|C_i|}{Z} = \frac{I_{pc}}{Z} \\
$$
式の意味
\( I_{pc} \)は、固有多項式の係数の平均情報エントロピーを用いて、分子の複雑さを表現しています。一般的に、分子の枝分かれが多くなるほど、\( I_{pc} \)が小さくなる傾向があるようです。
例えば、次のようなC5アルカンのIpcを計算してみます。
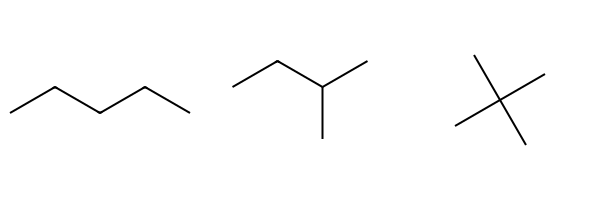
from rdkit import Chem
from rdkit.Chem import Draw, GraphDescriptors
mol1= Chem.MolFromSmiles("CCCCC")
mol2= Chem.MolFromSmiles("CCC(C)C")
mol3= Chem.MolFromSmiles("CC(C)(C)C")
print(GraphDescriptors.Ipc(mol1))
print(GraphDescriptors.Ipc(mol2))
print(GraphDescriptors.Ipc(mol3))
# <output>
# 11.245112497836532
# 9.65148445440323
# 3.6096404744368114結果、同じ原子数の化合物の場合、分子の枝分かれが多くなると、Ipcが小さくなることがわかります。
終わり。