BertzCTを理解する[RDKit記述子]

2024年7月11日

目的

RDKitに実装されているBertzCT 記述子を理解する。

BertzCT

RDKitのBertzCTは分子の複雑さを表した記述子であり、以下の論文を参考に定義されています。

Steven H. Bertz
Journal of the American Chemical Society 1981 103 (12), 3599-3601
DOI: 10.1021/ja00402a071

概要

BertzCT($ C_T $)は、分子の複雑さの指標として定義されています。
$ C_T $は、分子の結合の複雑さ$C(\eta) $と重原子の分布の複雑さ$ C(E) $の和で表されます。
つまり、
$$
C_T = C(\eta) + C(E)
$$
で計算されます。

分子の結合の複雑さ$C(\eta) $

$C(\eta) $は、分子の結合の複雑さを表現した指標です。
以下の式で計算されます。
$$
C(\eta) = 2\eta log_2 \eta – \sum_{i} \eta_i log_2 \eta_i
$$
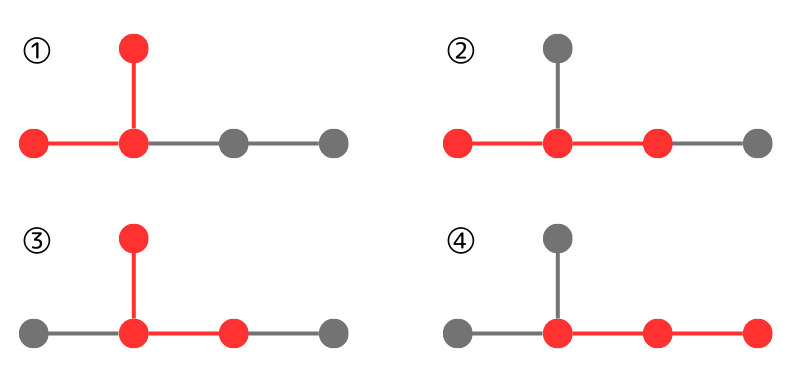
ここで、$ \eta $はGordon Mが1973年に定義した値を応用したものです。具体的には、分子グラフから連続した３原子(ノード)を何パターン切り取れるかという値です。例えば、下図のような2-メチルブタンのの場合、赤色でマークされた切り取り方が4パターン考えられるので$ \eta = 4 $となります。
また、$ \eta_i $はautomorphismな切り取り方を同じグループ $ i $として考えます。例えば、下図で②と③は対称性があるので同じグループとして数えます。そのため、$ \eta_i \in \{1,1,2 \} $となります。

Gordon M, et al.
J. Chem. Soc., Faraday Trans. 2, 1977,73, 1289-1307
DOI:10.1039/F29777301289

重原子の分布の複雑さ$ C(E) $

$ C(E) $は、重原子の分布の複雑さを表現した指標です。
以下の式で計算されます。
$$
C(E)= E log_2 E – \sum_{i} E_i log_2 E_i
$$
ここで、$E$は全原子の個数、$ E_i $は各原子種の個数である。
例えばアセトアミノフェン(C₈H₉NO₂)の場合、$ E = 8+1+2=11$、$ E_i \in \{8, 1, 2\} $となります。

式の意味

$C(\eta) $と$ C(E) $には、$ n log_2 n – \sum_{i} n_i log_2 n_i $ の形の式が含まれます。($C(\eta) $には、$ n log_2 n$がプラスされていますが)
$ p_i = n_i / n$としたとき、$ n log_2 n – \sum_{i} n_i log_2 n_i = – n \sum_{i} p_i log_2 p_i$となり、Shannonの情報エントロピのn倍で表されます。
つまり、結合種の分布や重原子の分布のばらつきを情報エントロピーを用いて表現していると考えられます。

終わり。